
Lecture notes (Fundamentals and Applications of FEM)
The lecture notes were prepared for an undergraduate course on the fundamentals and applications of the finite element method in solid mechanics.
You may make copies of these notes for education and research.
The lecture notes can be found here:
Predicting in-plane instability of high-speed rotating silicon multi-ring structures
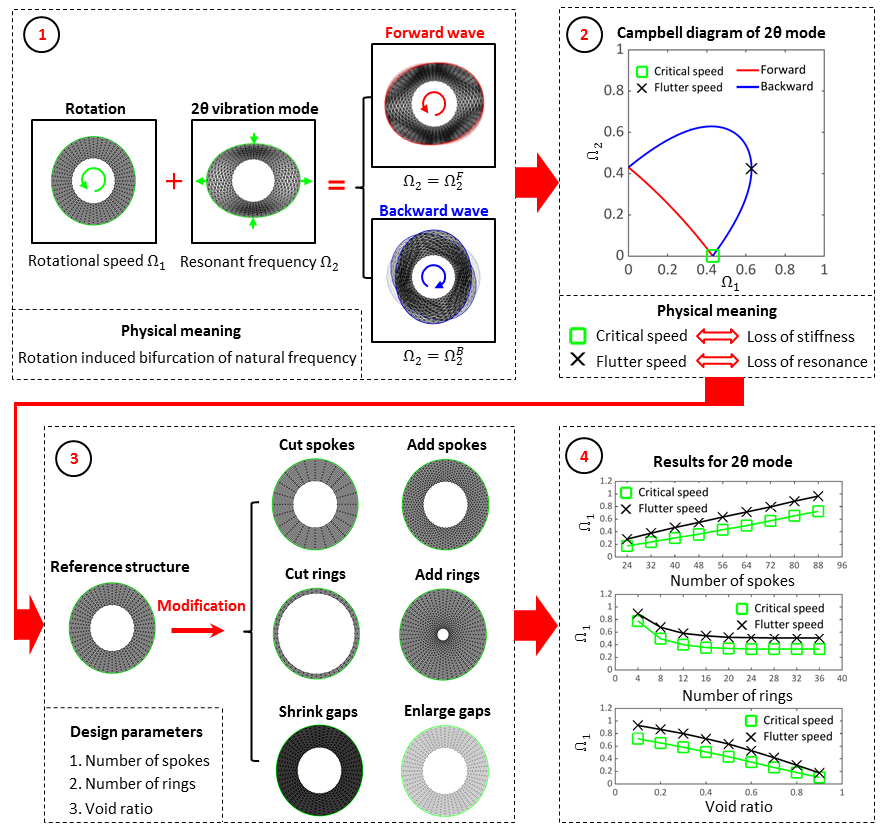
Silicon multi-ring structures connected by spokes are ideal candidate to carry circumferential traveling waves in the design of MEMS vibratory gyroscope. However, these structures are prone to instability at high-speed rotation. This paper presents an efficient approach to determine the critical and flutter speeds of these structures for their various natural modes, and thereby to predict their in-plane instability. Through extensive parametric study, the effects of various design parameters on the instability of these structures are obtained and discussed. The results show that stability of these structures could be enhanced by increasing number of spokes, reducing number of rings, and reducing gaps between rings. Furthermore, it is found that these structures are more stable with circumferential traveling waves with a larger nodal diameter.
On the electromechanical instability of polar elastomers
Based on a continuum theory that accounts for the underlying molecular physics of polar elastomers (PEs), a typical boundary value problem (BVP) is developed to analyze the electro-mechanical instability (EMI) of PEs with randomly distributed dielectric particles. Through extensive numerical simulations, the effects of various parameters such as particle volume fraction, particle size and enhancement factor related to polar groups on the critical voltage leading to EMI of PEs are investigated. The results are presented in 3D phase diagrams, which may better help researchers to understand EMI of PEs and guide them in synthesis, design, and application of PEs in the fields of chemistry, physics, bio-engineering, etc.

MMASC-0.0.2
MMASC is a nonlinear finite element package for simulating mechanical behaviors of soft composites subjected to external stimuli in a multi-physics context.
The main features of the package are as following:
It supports Tet/Hex meshes.
It is coded in modern Fortran and has an interface for UMAT/VUMAT, UEL/VUEL etc.
It supports multi-physics nonlinear analysis, either static or dynamic, either implicit or explicit.
It supports two-scale analysis with options of 3 different homogenization methods.
- Affine method
- Periodic method
- Mixed method
It has a unique math-core and is independent of external libraries.
The current released version is only for electromechanical coupling problems.
The following is an example about coupling electric field and displacement field analysis for rubber-like materials (such as elastomers and gels). The problem is defined as shown in Fig. 1.
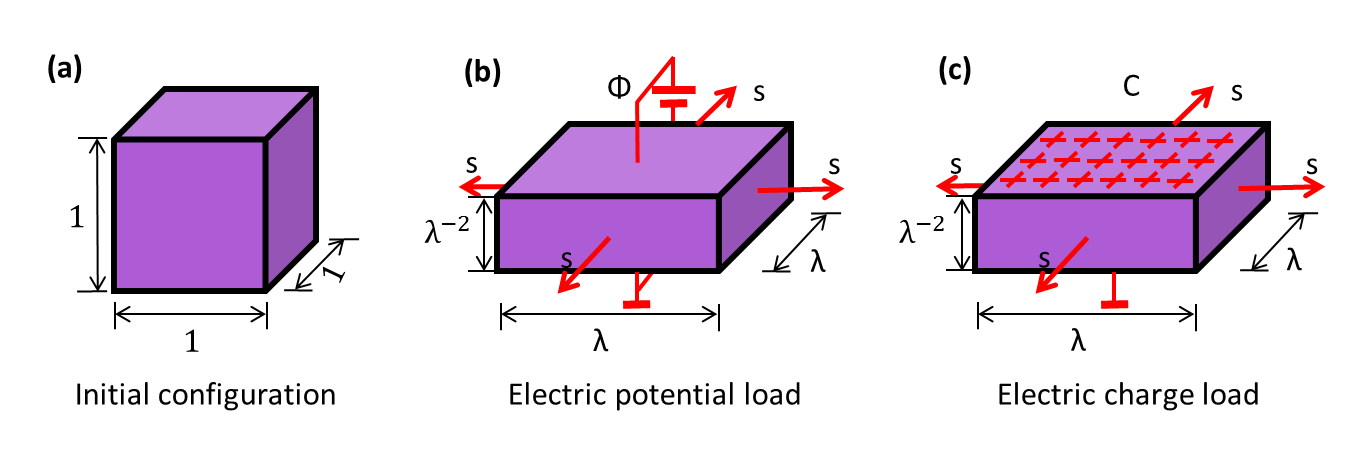
Four different analyses procedures (see Fig. 2) are incorporated into this version of MMASC, and each of the procedure defines two analysis steps.
The first step is controlled by mechanical pre-stress and the second step is controlled by electric potential or charge. In order to compare the two-scale procedure and one-scale procedure, this example just assumes that both macroscale domain and microscale unit cell are uniform. The results are shown in Fig. 3. While this example is simple, its extension to cases for heterogeneous materials is natural. Please consult to the user manual of MMASC.

You can find the program(Windows) here:
The input files for the example here:
You may download these 3 files in a folder and then open a terminal to run the program.
You are free to redistribute this version of MMASC. And I hope the program is helpful to your research.
UMATs for viscoelasticity
The source codes can be found here:
1 => Standard Viscoelasticity -> Arruda-Boyce solid + Newtonian fluid
2 => Standard Viscoelasticity -> Gent solid + Newtonian fluid
3 => Single element benchmarking
A demonstration:
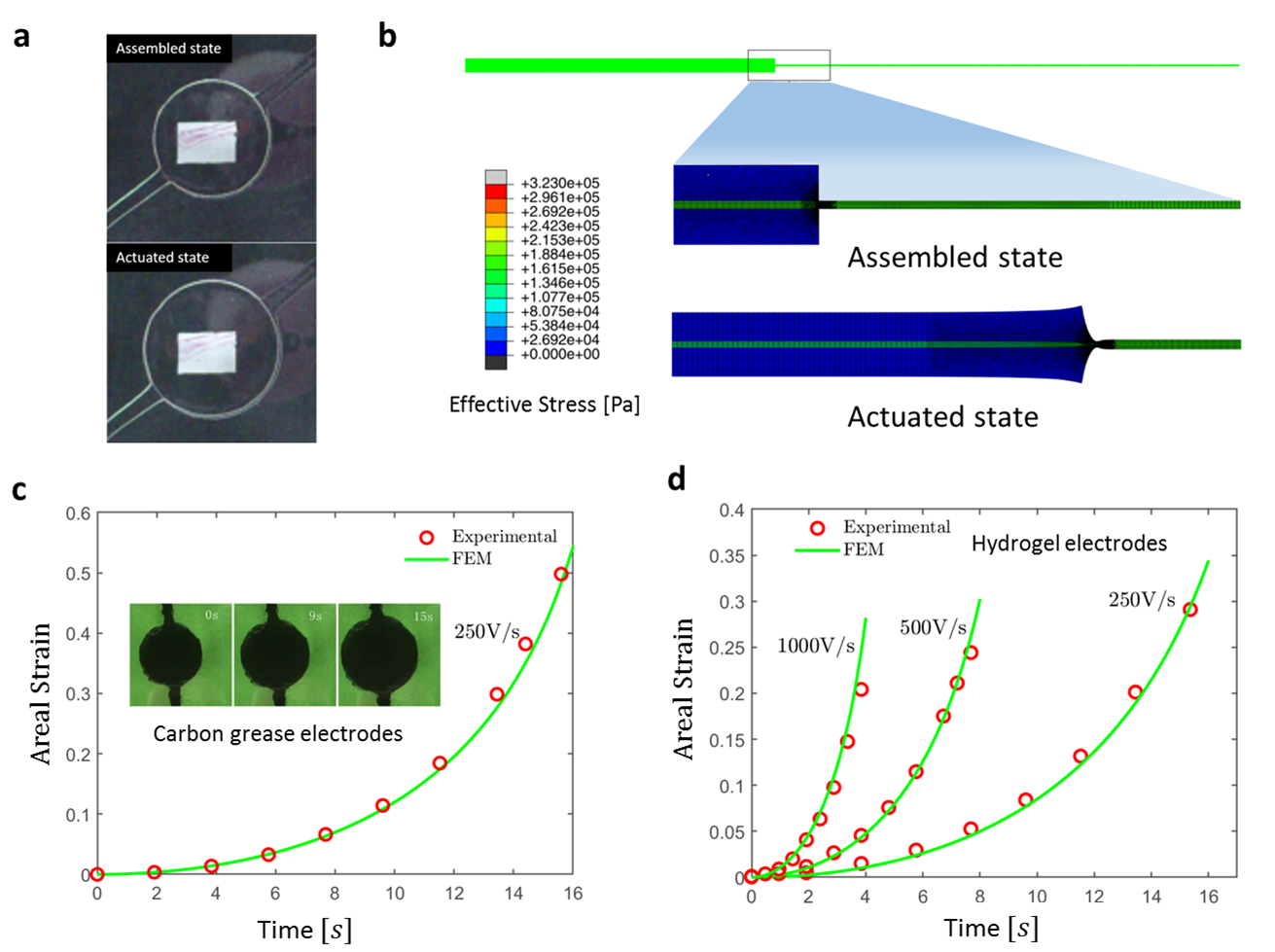
(a) showing experiment setup with hydrogel electrodes (b) showing the modeling in simulation (c) experimental and simulation results for canbon grease electrodes (d) for hydrogel electrodes
I hope these codes can also be used for educational purposes, other than research.
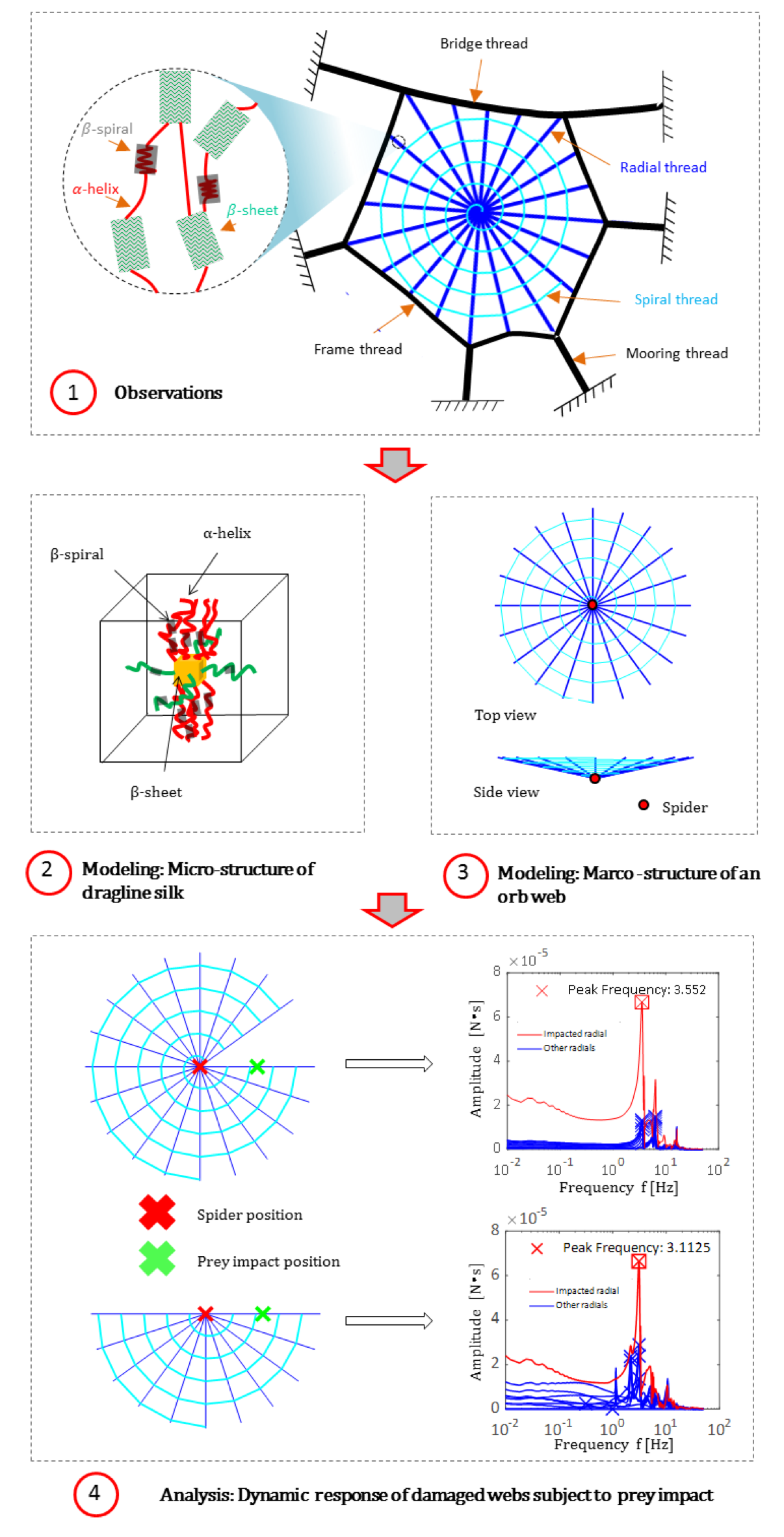
Dragline silk and spider orb webs
Some works on the modeling and analysis of spider orb webs under prey impact are presented as follows. More details can be found in the references. These works consist of my PhD thesis. It is challenging to achieve the end just in one year. Nevertheless, it was fullfilled. Sincere appreciation to my advisor Prof. Hashemi, the best professor that I have ever met.
I had been in USA for 5 years pursing a PhD. During the course, there were inevitably highs and lows. I drifted from the west coast to the east coast, meanwhile a short stay at Pittsburgh. The pale-yellow sunset in Los Angeles, the freezing-cold snow in Pittsburgh, and the viviflying Charles river in Boston were all borne in my mind. These scenes happen to map my feeling and experience in each place. All in all, the fifth year’s life in Boston is the most memoriable.
You can find a simulation movie here:
A theory of polar dielectric elastomers
Polar dielectric elastomers (PDEs) are electrically insulating soft materials where polar groups are chemically incorporated into material microstructures. These materials are pretty new and show promising applications, especially for low-electric-field driving soft robotics and devices, to name a few.
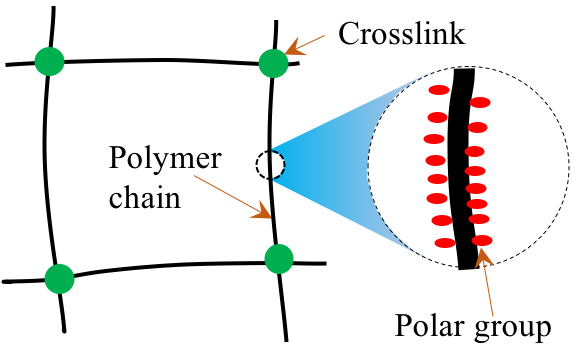
A schematic showing the microstructure of a polymer network with polar groups.
One prominent feature of PDEs is the dielectric permittivity enhancement effect of polar groups. In one of my recent papers, a mathematical formulation is proposed to shed light on the physical insight of the effect of polar groups. It is found that the effective dielectric constant is propotional to the fraction of polar groups per polymer chain in PDEs. Based on the finding, a concept called “dielectric imperfection” is proposed under the assumption of inhomogeneous distribution of polar groups in PDEs. A thorough discussion is given in a published paper.
This work and some relevant works were accomplised during a course of Independent Study at Northeastern University in the year 2018.
Elastomer lattices
The pictures below were taken in Apr. 2016. It can be appreciated purely from a aesthetical perspective without any rational pursuit.

The pictures below were taken in late 2016, showing a ferromagnetic elastomer octet-truss lattice is deformed subject to a magnetic field.
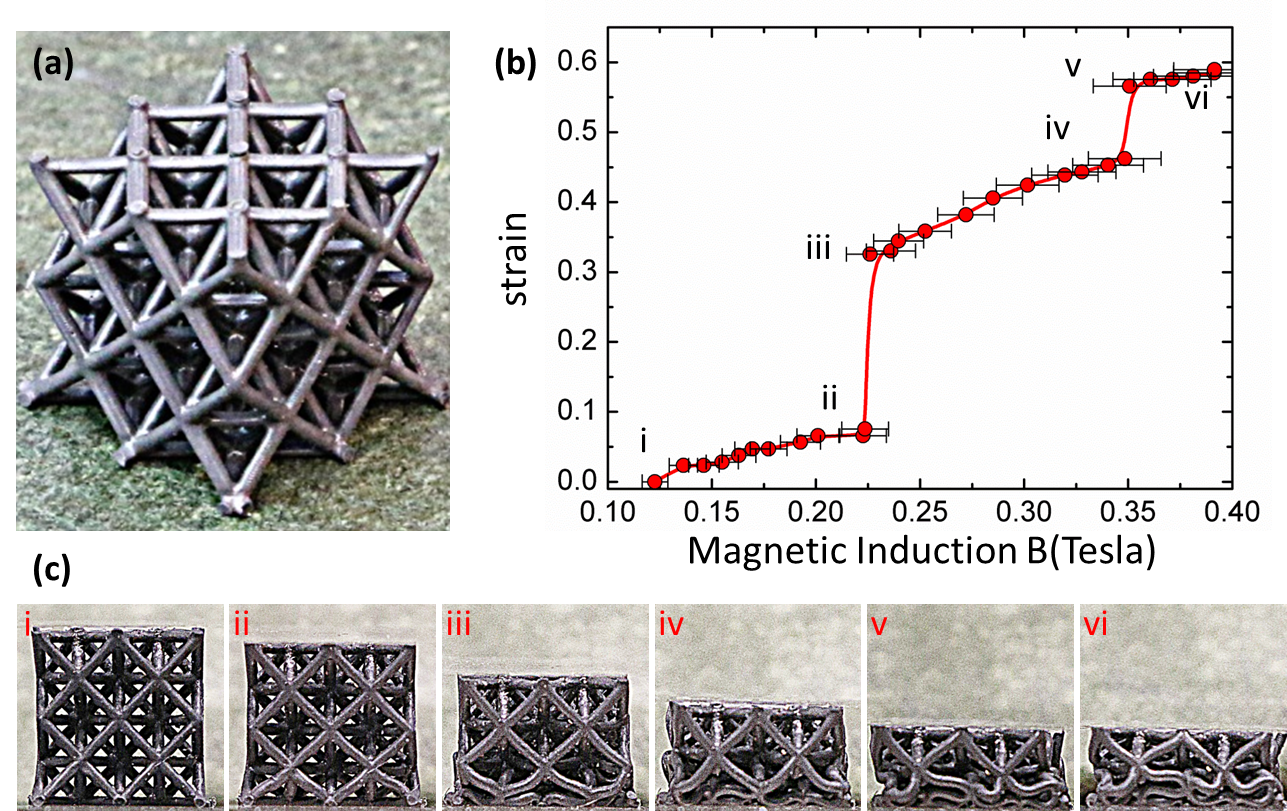
A technical report on the phenomena could be found here:
Magnetic Field Controlled Buckling and Post Buckling of an Inclined Beam